TRIGONOMETRY, ANGLES & DEGREES

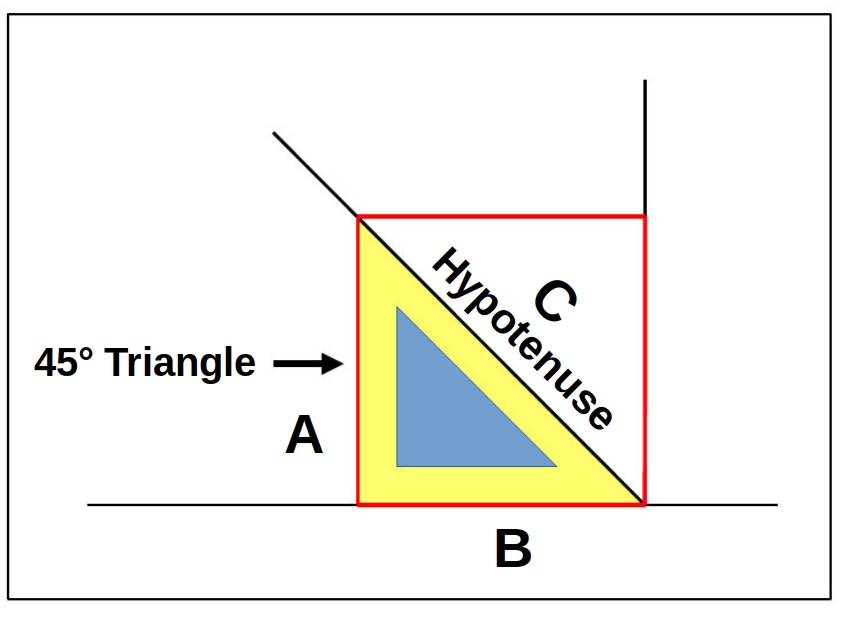
DISTANCE PROBLEM:   If a building is 300(91.44m) feet high & a bus stop is 800(731.52m) yards from the building, how far is it from the bus stop to the top of the building?

This forms what is called the "hypotenuse" of a right triangle

STEP 1: We need to sort out the relevant facts.

    1. The building is 300 feet high(91.44m).
    2. The bus stop is 800 yards(731.52m) from the building.
    3. The building is at a 90° angle from the ground.

STEP 2: We draw a 90° triangle and label the sides.

STEP 3: Convert 800 yards to feet (800 x 3) = 2400 feet

STEP 4: We apply the Pythagorean theorem: (paraphrased) - which states that: In a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.

(A²) + (B²) = (C²)

∴ (The symbol for therefore in math)

(A² = 300 x 300) or 90,000 +
(B² = 2400 x 2400) or 5,760,000 =
(C² = 90,000 + 5,760,000) or 5,850,000

(√ A²) + (√ B²) = (√ C²) or ( 2418.6773244) feet

As we can see, because, the building height is only 300 feet and the distance is 2400 feet. The hypotenuse is only about 18 feet longer than the ground distance to the bus stop

NOW LET'S DO IT THE EASY WAY!

We make 300 = 3 and 2400 = 24
We square 3 & 24 and get 9 + 576 = 585

The hypotenuse = The square root of (C²) or
(24.186773244)

Now all we have to do is move the decimal place two steps to the right and we get (2418.6773244)

A lot easier because the zeros can be removed, then added back.

AN ILLUSTRATION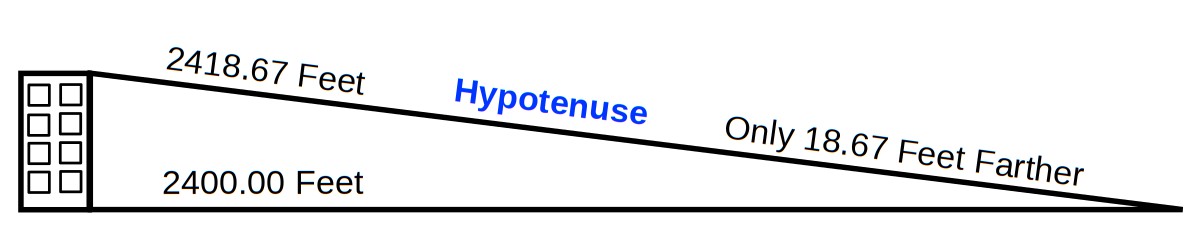

Metric & Imperial (a.k.a. feet & inches) measurements are often rounded to an "about" number.